众人都知说念麦克斯韦从麦克斯韦方程组里推导出了电磁波，然后通过缱绻发现电磁波的速率正巧等于光速。于是开云真人·(中国)入口-kaiyun开云最新App下载，麦克斯韦就预言“光是一种电磁波”，这个预言其后被赫兹说明。

电磁波的发现让麦克斯韦和他的电磁表面走上了神坛，也让东说念主类社会插足了无线电时间。你目下可以随时给远处的一又友打电话，能用手机看科学类著作，都跟电磁波有着密切的关系。那么，麦克斯韦到底是若何从麦克斯韦方程组推导出电磁波方程的呢？这篇著作咱们就来一说念见证这一古迹的时刻。

01什么是波？

要和会电磁波，领先咱们得了解什么是波？有些东说念主可能认为这个问题有点奇怪，什么是波这还用问么？我丢一块石头到水里，水面上就会变成一个水波；我抖动一根绳索，绳索上就会就会出现一个波动。生计中还有许多这种波动表象，我天然念书少，但是什么是波如故知说念的。

没错，水波、绳索上的波动这些都是波，我在这里抛出“什么是波？”这个问题并不是想来掰指头数一数哪些东西是波，哪些不是，而是想问：扫数这些叫作波的东西有什么共同的特征？咱们如何用一套拯救的数学话语来描摹波？

咱们研究物理，便是从万千变化的天然界的各式表象里总结出某种一致性，然后用数学的话语定量、精准的描摹这种一致的表象。目下咱们发现了水波、绳索上的波等许多表象都有这样一种波动表象，那咱们天然就要去寻找这种波动表象背后拯救的数学礼貌，也便是寻找描摹波动表象的方程，即波动方程。

为了寻找拯救的波动方程，咱们先来望望最毛糙的波：抖动一根绳索，绳索上就会出现一个波沿着绳索出动，以恒定的频率抖动就会出现伙同络续的波。

为了更好地研究绳索上的波动，咱们先缔造一个坐标系，然后把注释力齐集到其中的一个波上。于是，咱们就看到一个波以一定的速率v向x轴的正标的（右边）出动，如下图：

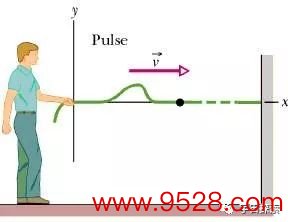
那么，咱们该如何去描摹这种波动呢？

领先，咱们知说念一个波是在不断地出动的，上图仅仅波在某个时刻的方式，它下一个时刻就会往右边出动少量。出动了些许也很好缱绻：因为波速为v，是以Δt时候以后这个波就会往右出动v·Δt的距离。

另外，我不论这个时刻波是什么形势的弧线，归正我可以把它行为一系列的点（x,y）的围聚，这样咱们就可以用一个函数y=f(x)来描摹它（函数便是一种对应（映射）关系，在函数y=f(x)里，每给定一个x，通过一定的操作f(x)就能得到一个y，这一双（x,y）就构成了坐标系里的一个点，把扫数这种点连起来就得到了一条弧线）。

然后，y=f(x)仅仅描摹某一个时刻的波的形势，要是咱们想描摹一个竣工动态的波，就得把时候t商量进来。也便是说咱们的波形是跟着时候变化的，即：我绳索上某个点的纵坐标y不仅跟横轴x相干，还跟时候t相干，这样的话咱们就得用一个二元函数y=f(x,t)来描摹一个波。

这一步很好和会，它无非告诉咱们波是随时候（t）和空间（x）变化的。但是这样还不够，寰球上到处都是跟着时候、空间变化的东西，比如苹果下降、篮球在天上飞，它们跟波的实质区别又在哪呢？

02波的实质

仔细想一下咱们就会发现：波在传播的时候，天然不同期刻波所在的位置不一样，但是它们的形势历久是一样的。也便是说前一秒波是这个形势，一秒之后波天然不在这个地点了，但是它依然是这个形势，这是一个很强的浪漫条目。有了这个浪漫条目，咱们就能把波和其它在时候、空间中变化的东西划分开了。

咱们这样商量：既然用f(x,t)来描摹波，那么波的驱动形势（t=0时的形势）就可以默示为f(x,0)。经过了时候t之后，波速为v，那么这个波就向右边出动了vt的距离，也便是把驱动形势f(x,0)往右出动了vt，那么这个赶走可以这样默示：f(x-vt,0)。

为什么把一个函数的图像往右出动了一段vt，赶走却是用函数的自变量x减去vt，而不是加上vt呢？这是一个中学数学问题，我这里稍稍帮众人追忆一下：你们想，要是我把一个函数图像f(x)往右出动了3，那么我蓝本在1这个地点的值f(1)，目下就成了4这个地点的函数值。是以，要是你还想用f(x)这个函数，那笃信就得用4减去3（这样才能得到f(1)的值），而不是加3（4+3=7，f(7)在这里可莫得什么意旨）。

是以，要是咱们用f(x,t)描摹波，那么驱动时刻（t=0）的波可以默示为f(x,0)。经逾期候t之后的波的图像就等于驱动时刻的图像往右出动了vt，也便是f(x-vt,0)。于是，咱们就可以从数学上给出波畅通的实质：

也便是说，只须有一个函数抖擞f(x,t)=f(x-vt,0)，抖擞轻易时刻的形势都等于驱动形势平移一段，那么它就默示一个波。水波、声波、绳索上的波、电磁波、引力波都是如斯，这也很合乎咱们对波的直不雅和会。

这里咱们是从纯数学的角度给出了波的一个描摹，底下咱们再从物理的角度来分析一下波的变成原因，望望能不成得到更多的信息。

03张力

一根绳索放在地上的时候是静止不动的，咱们甩一下就会出现一个波动。咱们想一想：这个波是若何传到远处去的呢？咱们的手仅仅拽着绳索的一端，并莫得遭遇绳索的中间，但是当这个波传到中间的时候绳索如实动了，绳索会动就默示有劲作用在它身上（牛爵爷告诉咱们的道理），那么这个力是那处来的呢？

稍稍分析一下咱们就会发现：这个力只能能来自绳索相邻点之间的互相作用，每个点把我方近邻的点“拉”一下，近邻的点就动了（就跟咱们排队报数的时候只见告你左右的阿谁东说念主一样）这种绳索里面之间的力叫张力。

张力的见地也很好和会，比如咱们用劲拉一根绳索，我明明对绳索施加了一个力，但是这根绳索为什么不会被拉长？跟我的手最近的阿谁点为什么不会被拉动？

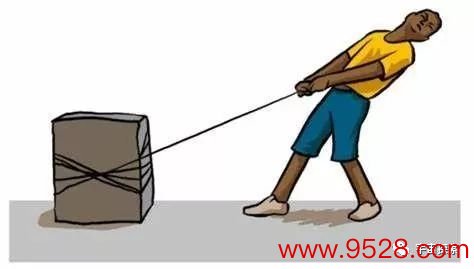
谜底天然是这个点足下的点给这个质点施加了一个相悖的张力，这样这个点一边被我拉，另一边被它相近的点拉，两个力的着力对消了。但是力的作用又是互相的，足下的点给端点施加了一个张力，那么这个足下的点也会受到一个来自端点的拉力，然而这个足下的点也没动，是以它也势必会受到更里面点的张力。这个经过可以一直传播下去，临了的赶走便是这跟绳索扫数的地点都会张力。

况兼，咱们还可以料定：要是绳索的质地忽略不计，绳索也莫得打结莫得被拉长，那么绳索里面的张力处处十分（只须有一个点双方的张力不等，那么这个点就应该被拉走了，绳索就会被拉变形），这是个很热切的论断。

通过上头的分析，咱们知说念了当一根梦想绳索处于紧绷情状的时候，绳索里面存在处处十分的张力。当一根绳索静止在大地的时候，它处于温存情状，莫得张力，但是当一个波传到这里的时候，绳索会变成一个波的形势，这时候就存在张力了。恰是这种张力让绳索上的点凹凸振动，是以，分析这种张力对绳索的影响就成了分析波动表象的时弊。

04波的受力分析

那么，咱们就从处于波动情状的绳索中聘用很小的一段AB，咱们来分析一下这个小段绳索在张力的作用下是如何畅通的。安适，咱们这里并不会波及什么复杂的物理公式，咱们所需要的公式就一个，大名鼎鼎的牛顿第二定律：F=ma。

牛顿第一定律告诉咱们“一个物体在不受力或者受到的合外力为0的时候会保握静止或者匀速直线畅通情状”，那么要是合外力不为0呢？牛顿第二定律就接着说了：要是合外力F不为零，那么物体就会有一个加快度a，它们之间的关系就由F=ma来定量描摹（m是物体的质地）。也便是说，要是咱们知说念一个物体的质地m，只须你能分析出它受到的合外力F，那么咱们就可以左证牛顿第二定律F=ma缱绻出它的加快度a，知说念加快度就知说念它接下来要若何动了。

牛顿第二定律就这样把一个物体的受力情况（F）和畅通情况（a）结合起来了，咱们想知说念一个物体是若何动的，只须去去分析它受到了什么力就行了，是以它牛。

再来看咱们的波，咱们从处于波动情状的绳索里收用很小的一段AB，咱们想知说念AB是若何畅通的，就要分析它受到的合外力。因为不商量绳索的质地，是以就无谓商量绳索的重力，那么，咱们就只须分析绳索AB两头的张力T就行了。

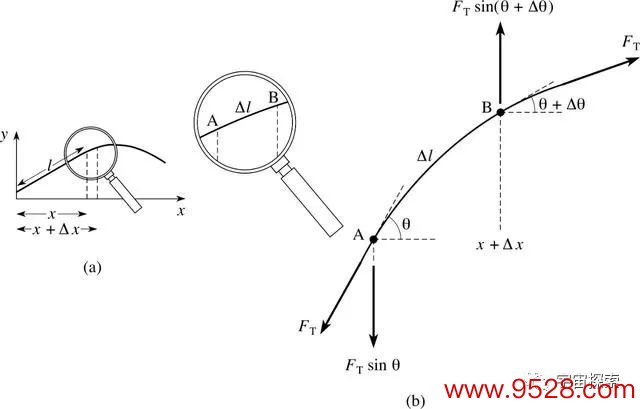
如上图，绳索AB受到A点朝左下方的张力T和B点朝右上方的张力T，况兼咱们还知说念这两个张力是十分的，是以才把它都记为T。但是，咱们知说念波动部分的绳索是迂曲的，那么这两个张力的标的是不一样的，这少量从图中可以相称彰着的看出来。咱们假定A点处张力的标的跟横轴夹角为θ，B点跟横轴的夹角就彰着不一样了，咱们记为θ+Δθ。

因为绳索上的点在波动时是凹凸畅通，是以咱们只商量张力T在凹凸方朝上的重量，水浩繁朝上的就不商量了。那么，咱们把AB两点的张力T都理解一下，稍稍用少量三角函数的学问咱们就能发现：A点出朝上的张力为T·sin（θ+Δθ），B点向下的张力为T·sinθ。那么，通盘AB段在竖直方朝上受到的协力就等于这两个力相减：F= T·sin（θ+Δθ）-T·sinθ。

好了，按照牛顿第二定律F=ma，咱们需要知说念物体的合外力F、质地m和加快度a，目下咱们还是知说念了合外力F，那么质地m和加快度a呢？

05波的质地分析

质地好说，咱们假定绳索单元长度的质地为μ，那么长度为Δl的绳索的质地便是μ·Δl。

但是，因为咱们取的是相称小的一段，咱们假定A点的横坐标为x，B点的横坐标为x+Δx，也便是说绳索AB在横坐标的投影长度为Δx，那么，当咱们取的绳长相称短的时候，咱们就可以近似用Δx代替Δl，这样绳索的质地就可以默示为：μ·Δx（本来我在商量这里要不要再解释一下微积分想想，但是一想，会看这篇电磁波篇的，必须是还是提前看了麦克斯韦方程组的积分篇和微分篇，而我在那两篇里还是先容过这种想想了，那这里就不说了~）。

质地责罚了，剩下的便是加快度a了。你可能以为我还是得到了合外力（F= T·sin（θ+Δθ）-T·sinθ）和质地m（μ·Δx），那么剩下笃信便是用合外力F除以质地m得到加快度a（牛顿第二定律），不不不，这样就不好玩了。咱们还可以从另一个角度来得到加快度a，然后把它们作为拼盘拼起来。从那处得到加快度呢a？从描摹波的函数f(x,t)里。

06波的加快度分析

不知说念众人还谨记咱们在前边说的这个描摹波的函数y=f(x,t)么？这个函数的值y默示的是在x这个地点，时候为t的时候这少量的纵坐标，也便是波的高度。咱们目下要求的也便是AB凹凸波动时的加快度，那么，若何从这个描摹点位置的函数里求出加快度a呢？

这里咱们再来和会一下加快度a，什么叫加快度？从名字就可以嗅觉到，这个量是用来掂量速率变化快慢的。加快度嘛，笃信是速率加得越快，加快度的值就越大。假如一辆车第1秒的速率是2m/s，第2秒的速率是4m/s，那么它的加快度便是用速率的差（4-2=2）除以时候差（2-1=1），赶走便是2m/s²。

再走动想一下，咱们是若何求一辆车的速率的？咱们是用距离的差来除以时候差的。比如一辆车第1秒钟距离起始20米，第2秒钟距离起始50米，那么它的速率便是用距离的差（50-20=30）除以时候差（2-1=1），赶走便是30m/s。

不知说念众人从这两个例子里发现了什么莫得？我用距离的差除以时候差就得到了速率，我再用速率的差除以时候差就得到了加快度，这两个经过都是除以时候差。那么，要是我把这两个经过合到一块呢？那是不是就可以说：距离的差除以一次时候差，再除以一次时候差就可以得到加快度？

这样表述并不是很准确，但是可以很通俗的让众人和会这个想想。要是把距离看作对于时候的函数，咱们对这个函数求一次导数（便是上头的距离差除以时候差，只不外趋于无限小）就得到了速率的函数，对速率的函数再求一次导数就得到了加快度的默示。是以，咱们把一个对于距离（位置）的函数对时候求两次导数，就可以得到加快度的抒发式。

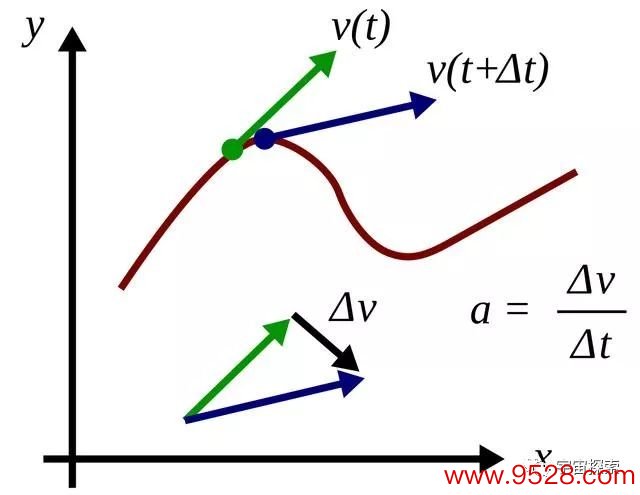
波的函数f(x,t)未便是描摹绳索上某少量在不同技巧t的位置么？那咱们对f(x,t)求两次对于时候的导数，天然就得到了这点的加快度a。因为函数f是对于x和t两个变量的函数，是以咱们只能时候的偏导∂f/ ∂t，再求一次偏导数就加个2上去。于是咱们就可以这样默示这点的加快度a=∂²f/ ∂t²（对于偏导数的先容，微分篇里有详确说明，这里不再说明）。

这样，咱们就把牛顿第二定律F=ma的三因素都凑王人了：F= T·sin（θ+Δθ）-T·sinθ，m=μ·Δx，a=∂²f/ ∂t²。把它们围聚在一说念就可以召唤神，阿不，就可以写出AB的畅通方程了：

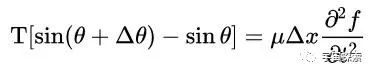
这个用牛顿第二定律写出来的波动方程，看起来若何样？嗯，似乎有点丑，看起来也不太澄澈，方程左边的东西看着太费事了，咱们还需要对它进行一番阅兵。那若何阅兵呢？咱们可以先把sinθ给干掉。

07方程的阅兵

为了大意凯旋地干掉sinθ，咱们先走动顾一下基本的三角函数：

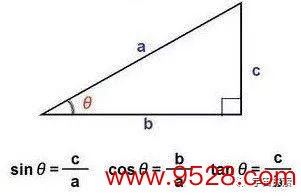
如上图，右边是一个直角三角形abc，那么角θ的正弦值sinθ等于对边c除以斜边a，正切值tanθ等于对边c除以邻边b。

当这个角度θ还很大的时候，a比b要彰着长一些。但是，一花旦度θ相称相称小，可以遐想，邻边b和斜边a就将近重合了。这时候咱们是可以近似的认为a和b是十分的，也便是a≈b，于是就有c/b≈c/a，即tanθ≈sinθ。

也便是说，在角度θ很小的时候，咱们可以用正切值tanθ代替正弦值sinθ。咱们假定这跟绳索的扰动相称小，形变相称小，那么θ和θ+Δθ就都相称小，那么它们的正弦值就都可以用正切值代替。于是，阿谁波动方程左边的sin(θ+Δθ)-sinθ就可以替换为：tan(θ+Δθ)-tanθ。

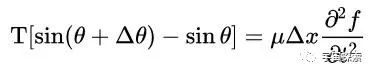
为什么咱们要用正切值tanθ代替正弦值sinθ呢？因为正切值tanθ还可以代表一条直线的斜率，代表弧线在某少量的导数。想想正切值的抒发式tanθ=c/b，要是建一个坐标系，那么这个c刚好便是直线在y轴的投影dy，b便是在x轴的投影dx，它们的比值刚好便是导数dy/dx，也便是说tanθ=dy/dx。

然而，因为波的函数f(x,t)是对于x和t的二元函数，是以咱们只能求某少量的偏导数，那么正切值就等于它在这个点的偏导数：tanθ=∂f/ ∂x。那么，蓝本的波动方程就可以写成这样：

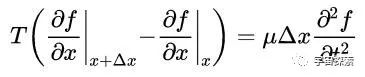
这里我稍稍解释一下偏导数的绚烂，咱们用∂f/ ∂x默示函数f(x,t)的偏导数，这是一个函数，x可以取各式种种的值。但是要是我加一个竖线|，然后在竖线的右下角标上x+Δx就默示我要求在x+Δx这个地点的导数。

再来看一下这个图，咱们还是商定了A点的横坐标为x，对应的角度为θ；B点的横坐标是x+Δx，对应的角度为θ+Δθ。是以，咱们可以用x+Δx和x这两处的偏导数值代替θ+Δθ和θ这两处的正切值tan（θ+Δθ）和tanθ，是以波动方程才可以写成上头那样：

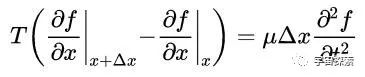
接着，要是咱们再对方程的双方同期除以Δx，那左边就变成了函数∂f/ ∂x在x+Δx和x这两处的值的差除以Δx，这其实便是∂f/ ∂x这个函数的导数抒发式。也便是说，双方同期除以一个Δx之后，左边就变成了偏导数∂f/ ∂x对x再求一次导数，那便是f(x,t)对x求二阶偏导数了。

上头咱们用咱们还是用∂²f/ ∂t²来默示函数对t的二阶偏导数，那么这里天然就可以用∂²f/ ∂x²来默示函数对x的二阶偏导数。然后双方再同期除以T，得到方程就简易多了：

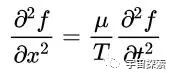
把方程左边的tan(θ+Δθ)-tanθ变成了函数f(x,t)对空间x的二阶偏导数，这个经过相称的热切，众人可以好好体会一下这个经过。正切值tanθ便是一阶导数，然后两个正切值的差除以自变量的变化就又产生了一次导数，于是统共就有了两阶，是以咱们才能得到上头阿谁简易的式子。

08经典波动方程

再望望方程右边的μ/T，要是你仔细去算一下μ/T的单元，你会发现它刚好便是速率的浩繁，也便是说要是咱们把一个量界说成μ/T的浩繁根，那么这个量的单元刚好便是速率的单元。可以遐想，这个速率天然便是这个波的传播速率v：

这样界说速率v之后，咱们最终的波动方程就可以亮相了：

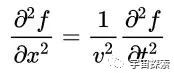
这个方程便是咱们最终要找的经典波动方程，为什么把它作作念佛典的波动方程呢？因为它莫得商量量子效应啊，在物理学里，经典就黑白量子的同义词。要是咱们要商量量子效应，这个经典的波动方程就没用了，咱们就必须转而使用量子的波动方程，那便是大名鼎鼎的薛定谔方程。

薛定谔便是从这个经典波动方程动身，结合德布罗意的物资波见地，硬猜出了薛定谔方程。这个方程让物理学家们从被海森堡的矩阵主宰的怯生生中解放了出来，再行回到了微分方程的好意思好寰球。薛定谔方程天然狠恶，但是它并莫得商量狭义相对论效应，而高速畅通（近光速）的粒子在微不雅寰球是很常见的，咱们也知说念当物体接近光速的时候就必须商量相对论效应，但是薛定谔方程并莫得作念到这少量。

最终让薛定谔方程相对论化是狄拉克，狄拉克把我方关在房间三个月，最终逼出了不异大名鼎鼎的狄拉克方程。狄拉克方程初度从表面上预言了反物资（正电子），天然其时的科学家们认为狄拉克这是在瞎闹，但是我国的物理学家赵忠尧先生却简直在同期就初度在施行室里不雅测到了正负电子灭亡的情况。

另外，狄拉克的责任也鼓吹了量子场论的降生，大开了一扇让东说念主无比赞佩的新寰球大门。物理学家们沿着这条路谨守了电磁力、强力、弱力，缔造起了粒子物理的圭臬模子，于是四海清平，六合大定，除了那活该的引力。这些精妙绝伦的故事咱们背面再讲，要是把这些故事写成一册《量子勇士传》，嗯，一定不比金庸的武侠失神~

好了，记忆正题，看到这个经典波动方程到背面还能掀翻那么大的浪来，是不是瞬息就对它骚然起敬了呢？咱们这样一顿操作推导出了经典波动方程，有的一又友可能有点懵，不紧要，咱们再来捋一下。这个看着很复杂的，包含了二阶偏导数的方程其实就仅仅告诉咱们：咱们把这跟绳索极小的一段看作一个质点，那么这个质点抖擞牛顿第二定律F=ma，仅此辛苦。

09复盘

咱们通盘推导经过不外便是去寻找F=ma中的这三个量。咱们把绳索的张力在竖直标的作念了理解，然后得到了它在竖直方朝上的协力F（T·sin（θ+Δθ）-T·sinθ）；咱们界说了单元长度的质地μ，然后就可以缱绻那小段绳索的质地m（μ·Δx）；咱们通过对波的函数f(x,t)的分析，发现要是对这种默示距离（位移）的函数对时候求一次偏导数就得到了速率，再求一次偏导数就得到了加快度，于是咱们就得到了这段绳索的加快度a（∂²f/ ∂t²）。然后咱们就把这些量按照牛顿第二定律F=ma拼了起来。

在处理问题的经过中，咱们作念了许多近似：因为咱们是取得很小的一段，那么咱们就可以用Δx近似代替绳索的长度Δl；假定扰动很小，绳索偏离x轴很小，那么角度θ就很小，咱们就近似用正切值tanθ代替正弦值sinθ。许多东说念主乍一看，认为这样严格的推导若何能这样高慢的近似呢？你这里近似那里近似，得到的最终赶走如故准确的么？

要和会这个问题，就得持重去学习微积分了，我目下告诉你微积分的中枢想想便是一种以直代曲的近似，你信么？微积分里便是用各式小段小段的直线去近似的代替弧线，但是得到的赶走却是相称精准的。因为咱们可以把这些线段取得相称相称的小，或者说是无限小，那么这个邪恶也就渐渐变成无限小了。是以咱们在分析这跟绳索的时候，也都强调了是取相称小的一段，给一个相称小的扰动，得到一个相称小的角度θ。

另外，tanθ便是一次导数，然后它们的差再除以一次Δx，就又出现了一次导数，是以方程的左边就出现了f(x,t)对位置x的两次偏导数。方程的右边便是函数f(x,t)对时候t求两次偏导数得到的加快度a（求一次导数得到速率，求两次就得到加快度）。

是以，天然咱们看到的是一个波动方程，其实它仅仅一个角色了的牛顿第二定律F=ma。和会这点，波动方程就没什么奇怪的了。咱们再来仔细的扫视一下这个方程：

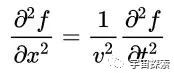
这个波动方程的意旨也很直不雅，它告诉咱们f(x,t)这样一个随时候t和空间x变化的函数，要是这个二元函数对空间x求两次导数得到的∂²f/ ∂x²和对时候t求两次导数得到的∂²f/ ∂t²之间抖擞上头的那种关系，那么f(x,t)描摹的便是一个波。

要是咱们去解这个方程，咱们得到的便是描摹波的函数f(x,t)。而咱们前边对波作念数学分析的时候得到了这样一个论断：要是一个函数f(x,t)描摹的波，那么就一定抖擞f(x,t)=f(x-vt,0)。是以，波动方程的解f(x,t)笃信也都抖擞前边这个关系，这少量感敬爱的一又友可以我方下去评释一下。

好了，经典的波动方程咱们就先讲到这里。有了波动方程，你会发现咱们通过几步毛糙的运算就能从麦克斯韦方程组中推导出电磁波的方程，然后还能笃信电磁波的速率。

10真空中的麦克斯韦方程组

麦克斯韦方程组的微分形势是这样的：

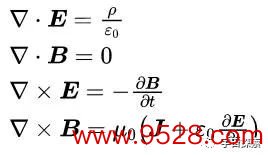
这组方程的一脉相承之前还是作念了详确的先容，这里不再多说。这组方程里，E默示电场强度，B默示磁感应强度，ρ默示电荷密度，J默示电流密度，ε0和μ0分别默示真空中的介电常数和磁导率（都是常数），▽是矢量微分算子，▽·和▽×分别默示散度和旋度：

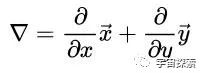
接下来咱们的任务，便是看如何从这组方程里推出电磁波的方程。

领先，要是果然能变成波，那么这个波笃信就要往听说，在隔离了电荷、电流（也便是莫得电荷、电流）的地点它还能我方传播。是以，咱们先让电荷密度ρ和电流密度J都等于0，当ρ=0，J=0时，咱们得到的便是真空中的麦克斯韦方程组：

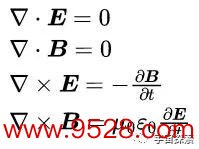
有些东说念主认为你若何能让电荷密度ρ等于0呢？这样第一个方程就成了电场的散度▽·E=0，那不就等于说电场强度E等于0，莫得电场了么？莫得电场还若何来的电磁波？

许多东说念主入门者都会有这样一种歪曲：好像认为电场的散度▽·E等于0了，那么就莫得电场了。其实，电场的散度等于0，仅仅告诉你通过包含这少量的无限小曲面的电通量为0，电通量为0不代表电场E为0啊，因为我可以收支这个曲面的电通量（电场线的数目）十分。这样有些许正的电通量（进去的电场线数目）就有些许负的电通量（出来的电场线数目），收支正负对消了，是以总的电通量如故0。于是，这点的散度▽·E就可以为0，而电场强度E却不为0。

是以这个众人一定要划分了了：电场E的散度为0不代表电场E为0，它仅仅要求电通量为0辛苦，磁场也一样。

这样咱们再来扫视一下真空中（ρ=0，J=0）的麦克斯韦方程组：方程1和2告诉咱们真空中电场和磁场的散度为0，方程3和4告诉咱们电场和磁场的旋度等于磁场和电场的变化率。前两个方程都是孤立的描摹电和磁，后两个方程则是电和磁之间的互相干系。咱们隐隐约约也能嗅觉到：要是要推导出电磁波的方程，你笃信得把上头几个式子笼统起来，因为波是要往听说的，而你上头单独的方程都仅仅描摹某少量的旋度或者散度。

有一个很毛糙的把它们都笼统在一说念的智力：对方程3和方程4双方同期再取一次旋度。

方程3的左边是电场的旋度▽×E，对它再取一次旋度就变成了▽×（▽×E）；方程3的右边是磁场的变化率，对右边取一次旋度也可以得到磁场B的旋度▽×B，这样不就刚好跟方程4讨论起来了么？对方程4双方取旋度看起来也一样，这看起来是个可以的兆头。

可能有些一又友会有一些疑问：你凭什么对方程3和4的双方取旋度，而不取散度呢？要是感敬爱你可以双方都取散度试试，你会发现电场E的旋度取散度▽·（▽×E）的赶走恒等于0。

这少量你看方程3 的右边会更了了，方程3的右边是磁场的变化率，你要是对方程左边取散度，那么右边也得取散度，而右边磁场的散度是恒为0的（▽·B=0便是方程2的内容）。这样就得不出什么专诚旨的赶走，你算出0=0能得到什么呢？

是以，咱们目下的问题变成了：如何求电场E的旋度的旋度（▽×（▽×E））？因为旋度毕竟和叉乘密切相干，是以咱们如故先来望望叉乘的叉乘。

11叉乘的叉乘

在积分篇和微分篇里，我还是跟众人详确先容了矢量的点乘和叉乘，况兼咱们还知说念点乘的赶走A·B是一个标量，而叉乘的赶走A×B是一个矢量（标的可以用右手定章来判断，右手从A指向B，大拇指的标的便是A×B的标的）。

而点乘和叉乘都是矢量之间的运算，那么A·B的赶走是一个标量，它就不成再和其它的矢量进行点乘或者叉乘了。但是，A×B的赶走仍然是一个矢量啊，那么按照道理它还可以连续跟新的矢量进行点乘或者叉乘运算，这样咱们的运算就可以有三个矢量参与，这种赶走咱们就称为三重积。

A·（B×C）的赶走是一个标量，是以这叫标量三重积；A×（B×C）的赶走如故一个矢量，它叫矢量三重积。

标量三重积A·（B×C）其实很毛糙，我在微分篇说过，两个矢量的叉乘的大小等于它们构成的平行四边形的面积，那么这个面积再和一个矢量点乘一把，你会发现这刚好便是三个矢量A、B、C构成的平行六面体的体积。

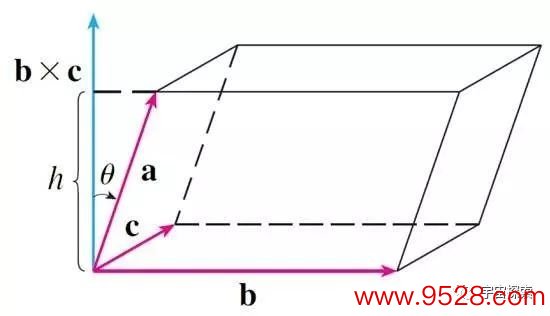
这个众人对着上头的图稍稍一想就会明白。况兼，既然是体积，那么你高慢更换它们的措施笃信都不会影响最终的赶走。咱们真实要要点商量的，如故矢量三重积。

矢量三重积A×（B×C），跟咱们上头说电场E旋度的旋度▽×（▽×E）形势相近，密切相干。它莫得上头标量三重积那样毛糙直不雅的几何意旨，咱们好像只能从数学上去推导，这个推导经过，哎，我如故径直写赶走吧：

A×（B×C）=B（A·C）-C（A·B）。

赶走是这样个东西，是不是很出丑？嗯，如实有点丑。不外记这个公式有个毛糙的口诀：纵横阖捭。什么叫纵横阖捭呢？昔时秦相范雎，啊不，A×（B×C）里的A距离B近一些，距离C远一些，是以A要齐集C（A·C前边的合乎是正号）攻打B（A·B前边的绚烂是负号），这样这个公式就好记了，感敬爱的可以我方去完成推导的经过。

12旋度的旋度

有了矢量三重积的公式，咱们就来比葫芦画瓢，来套一套电场E的旋度的旋度▽×（▽×E）。咱们对比一下这两个式子A×（B×C）和▽×（▽×E），好像只须把A和B都换成▽，把C换成E就行了。那么，矢量三重积的公式（A×（B×C）=B（A·C）-C（A·B））就变成了：

▽×（▽×E）=▽（▽·E）-E（▽·▽）。

嗯，▽（▽·E）默示电场E的散度的梯度，散度▽·E的赶走是一个标量，标量的梯度的专诚旨的，但是背面阿谁E（▽·▽）是什么鬼？两个▽算子挤在一说念，中间如故一个点乘的绚烂，看起来好像是在求▽的散度（▽·），但是▽是一个算子，又不是一个矢量函数，你若何求它的散度？况兼两个▽前边有一个电场E，若何E还跑到▽算子的前边去了？

咱们再看一下矢量三重积的公式的背面一项C（A·B）。这个式子的真理是矢量A和B先进行点乘，点乘的赶走A·B是一个标量，然后这个标量再跟矢量C相乘。很光显的，要是是一个标量和一个矢量相乘，那么这个标量放在矢量的前边背面都无所谓（3C=C3），也便是说C（A·B）=（A·B）C。

那么，不异的，E（▽·▽）就可以换成（▽·▽）E，而它还可以写成▽²E，这样就攀扯出了另一个大名鼎鼎的东西：拉普拉斯算子▽²。

13拉普拉斯算子▽²

拉普拉斯算子▽²在物理学界可谓大名鼎鼎，它看起来好像是哈密顿算子▽的浩繁，其实它的界说是梯度的散度。

咱们假定空间上少量（x,y,z）的温度由T（x,y,z）来默示，那么这个温度函数T（x,y,z）便是一个标量函数，咱们可以对它取梯度▽T，因为梯度是一个矢量（梯度有标的，指向变化最快的阿谁标的），是以咱们可以再对它取散度▽·。

咱们诈欺咱们在微分篇学的▽算子的伸开式和矢量坐标乘法的规则，咱们就可以把温度函数T（x,y,z）的梯度的散度（也便是▽²T）默示出来：

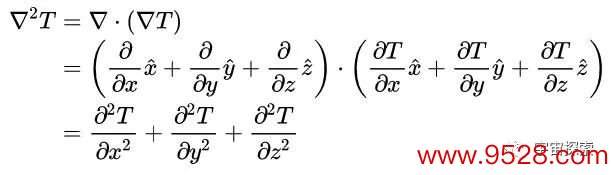
再对比一下三维的▽算子：

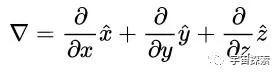
是以，咱们把上头的赶走（梯度的散度）写成▽²亦然相称容易和会的，它跟▽算子的鉴别也便是每项多了一个浩繁。于是，拉普拉斯算子▽²就天然可以写成这样：

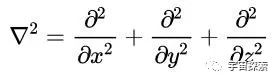
从拉普拉斯算子▽²的界说咱们可以看到，似乎它只能对作用于标量函数（因为你要先取梯度），但是咱们把▽²稍稍扩展一下，就能让它也作用于矢量函数V（x,y,z）。咱们只须让矢量函数的每个重量分别去取▽²，就可以界说矢量函数的▽²：

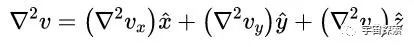
界说了矢量函数的拉普拉斯算子，咱们稍稍注释一下底下的这个论断（课下我方去评释）：

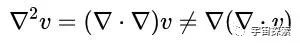
然后再望望中间的阿谁东西，是不是有点眼熟？

咱们在求电场旋度的旋度的时候，不就刚好出现了（▽·▽）E这个东西么？目下咱们就可以直来直去地把它替换成▽²E了，于是，电场旋度的旋度就可以写成这样：

▽×（▽×E）=▽（▽·E）-（▽·▽）E=▽（▽·E）-▽²E。

至此，咱们诈欺矢量的三重积公式推电场E的旋度的旋度的经过就竣事了，然后咱们就得到了这个极其热切的论断：

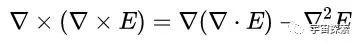
它告诉咱们：电场的旋度的旋度等于电场散度的梯度减去电场的拉普拉斯。有了它，电磁波的方程立马就可以推出来了。

14见证古迹的时刻

咱们再来望望真空中的麦克斯韦方程组：

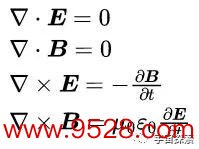
它的第三个方程，也便是法拉第定律是这样默示的：

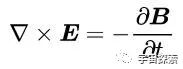
咱们对这个公式双方都取旋度，左边便是上头的论断，右边无非便是对磁感应强度B取个旋度，即：

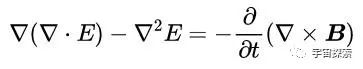
你望望这几项，再望望真空中的麦克斯韦方程组：方程1告诉咱们▽·E=0，方程4告诉咱们▽×B=μ0ε0（∂E/ ∂t），咱们把这两项代入到上头的式子中去，那赶走天然就变成了：

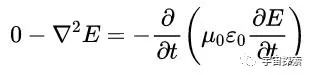
μ0、ε0都是常数，那右边天然就变成了对电场E求两次偏导。再把负号整理一下，临了的式子便是这样：

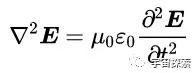
嗯，于是咱们就神奇般的把磁感应强度B消掉了，让这个方程只包含电场E。咱们再对比一下咱们之前絮聒了那么多得出的经典波动方程：

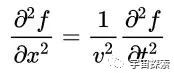
咱们在推导经典波动方程的时候只商量了一维的情况，因为咱们只商量波沿着绳索这一个维度传播的情况，是以咱们的赶走里独一∂²f/ ∂x²这一项。要是咱们商量三维的情况，那么不难遐想波动方程的左边应该写成三项，这三项刚好便是f的三维拉普拉斯：

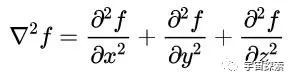
是以咱们的经典波动方程其实可以用拉普拉斯算子写成如下更普适的形势：

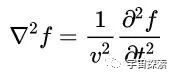
再望望咱们刚刚从麦克斯韦方程组中得到的电场方程：

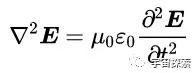
嗯，咱们推出的电场的方程跟经典波动方程的形势是一模一样的，目下咱们说电场E是一个波，你还有任何异议么？

咱们把电场E变成了一个孤立的方程，代价是这个方程变成了二阶（方程出现了浩繁项）的。对于磁场，一样的操作，咱们对真空中麦克斯韦方程组的方程4（▽×B=μ0ε0（∂E/ ∂t））双方取旋度，再重叠一次上头的经过，就会得到孤立的磁感应强度B的方程：

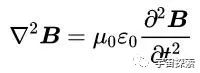
这样，咱们就发现E和B都抖擞波动方程，也便是说电场、磁场都以波动的形势在空间中传播，这天然便是电磁波了。

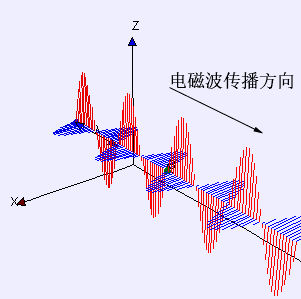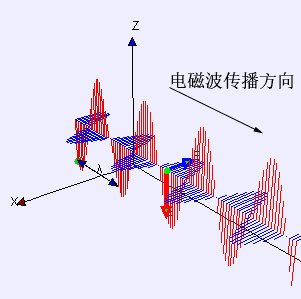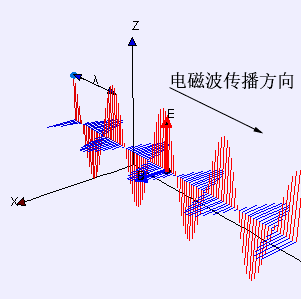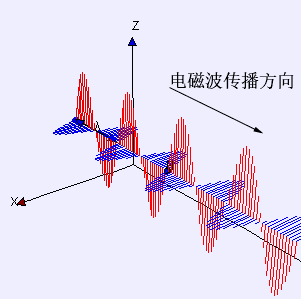
15电磁波的速率

对比一下电场和磁场的波动方程，你会发现它们是形势是一模一样的（便是把E和B互换了一下），这样，它们的波速也应该是一样的。对比一下经典波动方程的速率项，电磁波的速率v天然便是这样：

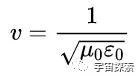
咱们去查一下μ0、ε0的数值，μ0=4π×10^-7N/A²，ε0=8.854187818×10^ -12 (F/m)，代入进去算一算：

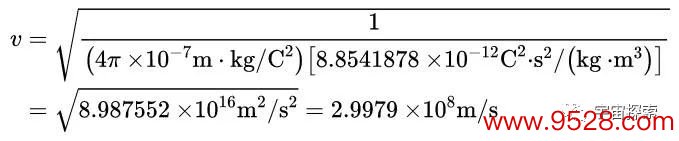
再查一下真空中的光速 c=299792458m/s。

前者是咱们从麦克斯韦方程组算出来的电磁波的速率，后者是从施行里测出来的光速。有这样的数据作念复古，麦克斯韦昔时才敢果敢的忖度：光便是一种电磁波。

天然，“光是一种电磁波”在咱们目下看来并不少见，但是你追忆一下历史：科学家们是在研究各式电表象的时候引入了真空介电常数ε0，在研究磁铁的时候引入了真空磁导率μ0，它们根底就跟光无关。麦克斯韦基于表面的好意思学和他惊东说念主的数学才能，提倡了位移电流假说（从推导里咱们也可以看到：要是莫得麦克斯韦加入的位移电流这一项，是不会有电磁波的），预言了电磁波，然后发现电磁波的速率只跟μ0、ε0相干，还刚好就等于东说念主们测量的光速，这如何能不让东说念主忌惮？

麦克斯韦一直以为我方在研究电磁表面，但是当他的电磁大厦落成时，他却未必地发现光的问题也被顺遂解决了，蓝本他一直在盖的是电磁光大厦。搞表面研究还可以买二送一，打折促销力度如斯之大，惊不惊喜，意不料外？

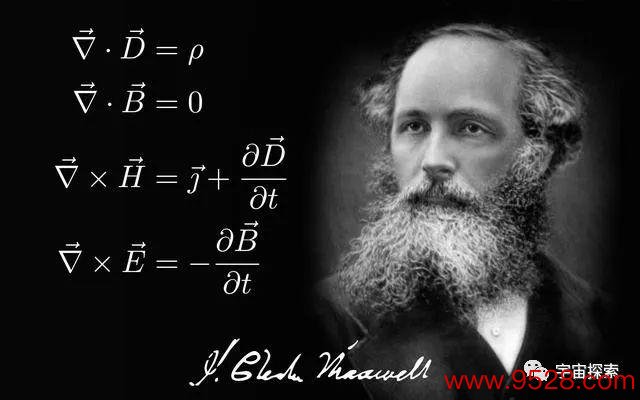
总之，麦克斯韦信赖我方的方程，信赖光是一种电磁波，当赫兹最终在施行室里发现了电磁波，并说明它的速率如实等于光速之后，麦克斯韦和他的表面得回了无上的荣耀。爱因斯坦其后却因为不太信赖我方的方程（认为六合不可能在推广）转而去修改了它，于是他就错失了预言六合推广的契机。当其后哈勃用千里镜不雅测到六合如确切推广时，爱因斯坦为此恼恨不已。

16结语

追忆一下电磁波的推导经过，咱们便是在真空麦克斯韦方程组的方程3和方程4的双方取旋度，然后就很天然的得出了电磁波的方程，然后得到了电磁波的速率等于光速c。这里有一个很时弊的问题：这个电磁波的速率是相对谁的？相对哪个参考系而言的？

在牛顿力学里，咱们说一个物体的速率，笃信是相对某个参考系而言的。你说高铁的速率是300km/h，这是相对大地的，你相对太阳那速率就大了。这个道理在咱们前边接洽的波那里也一样，咱们说波的速率一般都是这个波相对于它所在介质的速率：比如绳索上的波通过绳索传播，这个速率便是相对于绳索而言的；水波是在波在水里传播，那么这个速率便是相对水而言的；声波是波在空气里传播（真空宛转不到声息），声波的速率就天然是相对空气的速率。

那么，电磁波呢，从麦克斯韦方程组推导出的电磁波的速率是相对谁的？水？空气？光显都不是，因为电磁波并不需要水或者空气这种实体介质才能传播，它在真空中也能传播，否则你是若何看到太阳光和六合深处的星光的？况兼咱们在推导电磁波的经过中也根本莫得预设任何参考系。

于是其时的物理学家们就假定电磁波的介质是一种遍布空间的叫作“以太”的东西，于是众人入手去寻找以太，但是若何找都找不到。另一方面，电磁波的发现极大地支握了麦克斯韦的电磁表面，但是它跟牛顿力学之间却存在着根本矛盾，这种情况像极了目下广义相对论和量子力学之间的矛盾。若何办呢？

1879年，麦克斯韦死亡，同庚，爱因斯坦降生，这仿佛是两代伟东说念主的一个叮咛庆典。麦克斯韦电磁表面与牛顿力学之间的矛盾，以及“以太”这个大坑都被年青的爱因斯坦责罚了，爱因斯坦责罚它们的智力便是大名鼎鼎的狭义相对论。其实，当麦克斯韦把他的电磁表面提倡来之后，狭义相对论的问世就简直是势必的了，因为麦克斯韦的电磁表面其实便是狭义相对论框架下的表面，这亦然它跟牛顿力学打破的中枢。是以，爱因斯坦才会把他狭义相对论的论文取名为《论动体的电能源学》。

麦克斯韦的电磁表面竣事了一个时间，却又开启了一个新时间（相对论时间），它跟牛顿力学到底有什么矛盾？为什么非得狭义相对论才能解决这种矛盾？这些将是我背面要接洽的要点。我会勤奋让众人看到科学的发展有它澄澈的内在逻辑和原因，并不是谁拍拍脑袋就提倡一个惊天动地的新表面出来的。

此外，电磁表面和牛顿力学的交融是东说念主类解决两个相称告捷却又径直打破表面的一次相称珍藏的教育，这跟咱们目下边临的问题（广义相对论和量子力学的打破）相称肖似。我但愿大意通过这种说明给心爱科学的少年们一些启示，让他们以背靠近广义相对论和量子力学打破的时候，大意有一些灵感。

嗯，没错，我在期待将来的爱因斯坦~